Fundamentos da Informática – Circuitos Lógicos – 2

Neste artigo vou demonstrar circuitos simples, como os somadores. O objetivo não é falar de somador, mas sim mostrar um pouco da lógica da coisa.

Todo mundo sabe que, em binário, quando estamos trabalhando somente com 1 bit de precisão, 1+1 = 0. Mas, como fazer um circuito que calcule isto?

Se você leu os artigos anterior, aprendeu que a soma binária ocorre bit a bit, e o overflow é adicionado ao próximo elemento.

Um circuito somador precisa somar 2 valores binários. É necessário ainda, que o sistema avise quando ocorre um overflow. Considerando que nosso sistema é capaz de trabalhar apenas com valores de 1 bit (1 bit em cada uma das duas entradas, 1 bit de saida), vamos analizar a soma:

0+0=0, e não há overflow.

1+0 (ou 0+1), = 1, e não há overflow.

1+1=10. Como 10 são 2 bits, há overflow: 1+1=0 com overflow.

Logo,nosso circuito deve ser capaz de realizar a soma e avisar a ocorrência de um overflow.

Um desenho que se adequa as nossas necessidades é este:

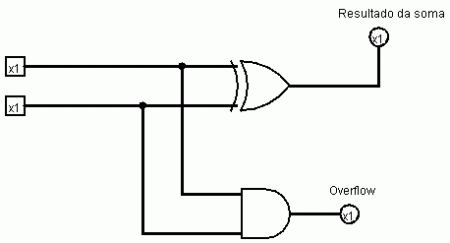
Observe: 0+1:

E agora 1+1:

Este circuito realiza a soma de forma correta.  Porém, ele soma somente 2 bits, ele não é muito util. Seria interessante se desse para construir um circuito que, além dos 2 valores de entrada, recebesse  um terceiro valor de entrada. Se ligar-mos este terceiro valor de entrada na saida de overflow de outro circuito somador, teremos um circuito de soma genérico – basta apenas cascatear os circuitos para somar vários bits. E é isto que iremos fazer agora:

Um circuito somador completo possui esta caracteristica, e pode ser representado da seguinte forma:

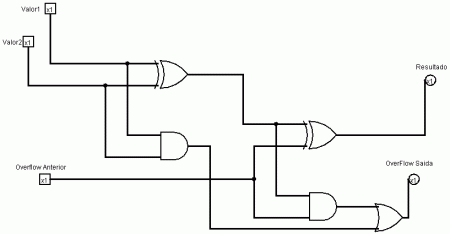
Por questões de espaço não vou mostrar cada um dos estados possiveis.

A questão é a seguinte: Este somador soma 2 valores de 1 bit, emitindo o resultado com 1 bit e se houve ou nao overflow. Ele também possui uma terceira entrada, que representa o valor do “Overflow Anterior”. Se ligar-mos em série vários cirtuitos destes, podemos somar 2 valores de mais de 1 bit, como o seguinte circuito, que soma 2 valores (A e B) de 2 bits cada:

O desenho ficou um pouco confuso pois eu fui obrigado a reduzir para caber no post.

Para facilitar, colocarei 2 exemplo: A soma de 01 + 01:

Observe que o valor de Overflow é transferido para a entrada de overflow do proximo circuito – exatamente como se faz na soma manual. Mas, e quando 11+01 for somado? O resultado é 100, que é muito grande para a precisão de 2 bits que este circuito possui. Nesta situação, ocorre o seguinte:

Observe que o Overflow passou a ser 1, enquanto o resultado 00. Esta soma esta correta.

Para fazer um circuito capaz de somar 3, 4, 10, 1000, 10209193123 bits, basta ir interligando os circuitos.

É importante lembrar que, o mesmo circuito de soma, é usado para subtração – a subtração é a a mesma operação de soma, porém com o segundo valor multiplicado por -1 (ou seja: 2 – 5 é o mesmo que 2 + (-5)).

O logisim possui uma função pré-pronta para representar o somador (há também para a subtração, multiplicação e divisão), o simbolo é:

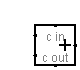
O mesmo circuito do somador de 2 bits pode ser feito da seguinte forma:

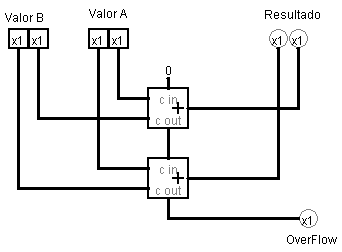
Que é bem mais simples de entender! O logisim possui a capacidade de fazer somadores de 2, 3, 4, até 32 bits nativamente. Se usarmos a técnica de combinação mostrada acima, é possivel criar circuitos para calcular qualquer quantidade de bits.